Part II: brains to bytes - journey from neurons to perceptrons
inspo from biological neurons
imagine your brain as a bustling metropolis, with trillions of neurons playing the role of its inhabitants.
these neurons are the ultimate multitaskers, constantly processing information, making decisions, and passing on messages.
here’s the deal:
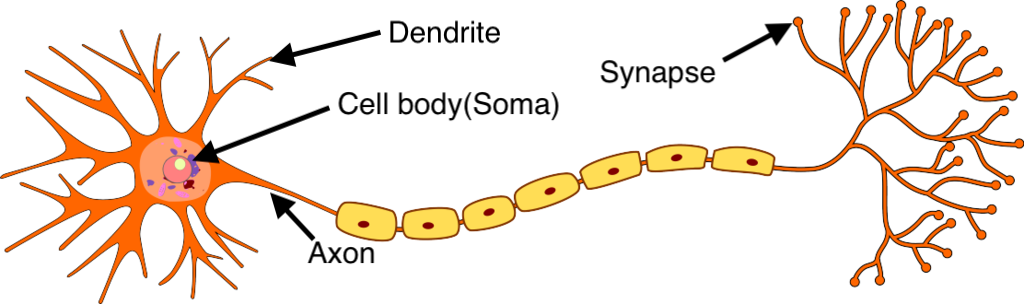
dendrites are like antennas, receiving signals from other neurons.
synapses are the connection points where neurons “talk” to each other.
soma processes the incoming signals, like a central office handling information.
axons transmit the processed signal to the next set of neurons.
this interconnected network forms a hierarchy. at the base, neurons might detect simple edges or corners (think: your brain spotting the outline of a cat).
higher up, they start combining this information to recognize patterns or even, say, a fluffy tail.
meet the mcculloch pitts neuron - the first artificial brain cell
in 1943, warren mcculloch and walter pitts proposed a simplified computational model of a neuron.
called the mcculloch pitts (MP) Neuron which laid the groundwork for modern neural networks.
the MP neuron isn’t as fancy as its biological counterpart, but it does the job.
here’s how it works:
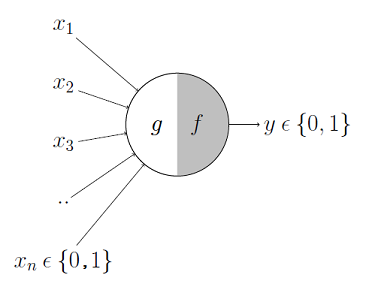
- it takes a bunch of binary inputs (0s and 1s) from its environment.
- each input can either excite or inhibit the neuron.
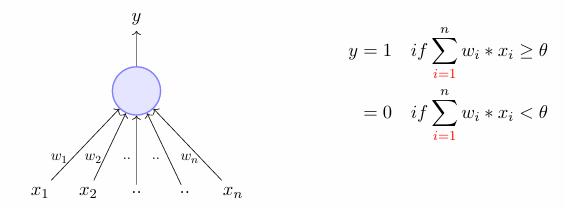
- it aggregates these inputs using a function 𝑔(𝑥), which is essentially the sum of the inputs.
- it compares this sum to a threshold 𝜃.
- if 𝑔(𝑥) >= 𝜃, the neuron “fires” (output = 1).
otherwise, it stays quiet (output = 0).
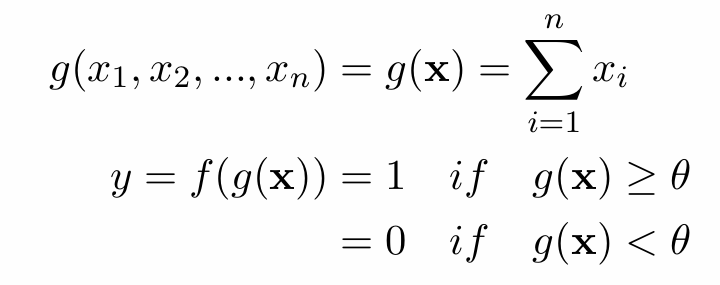
for example, if we fix a threshold 𝜃 = 3, the mp neuron fires only when atleast 3 of the xi’s are 1.
this process is called thresholding logic, and it’s surprisingly powerful.
boolean Functions and the MP Neuron
an MP neuron has two main parts:
- aggregation: the neuron sums its inputs, optionally weighted.
- thresholding: it outputs 1 if the sum exceeds a threshold value (θ), otherwise 0.
mathematically:
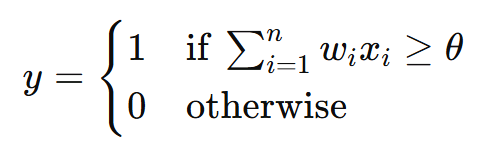
Here:
𝑥𝑖 : input values (0 or 1 for Boolean functions)
𝑤𝑖 : weights (can be binary or real numbers)
𝜃 : threshold
can a single mp neuron do it all?
the mcculloch-pitts (mp) neuron is a fundamental computational model of a neuron. its simplicity allows us to explore basic boolean functions and understand the limits of single-layer neural networks.
- and function
- the neuron fires only if all inputs are 1.
- parameters:
- weights (𝑤1, 𝑤2,…): 1, 1,… (all equal to 1).
- threshold (𝜃): number of inputs, 𝑛.
- weights (𝑤1, 𝑤2,…): 1, 1,… (all equal to 1).
- why? the total sum of inputs needs to match 𝑛 to output 1.
- e.g. neuron fires only when 𝑥1 + 𝑥2 + 𝑥3 = 3 because 𝑛 = 3.
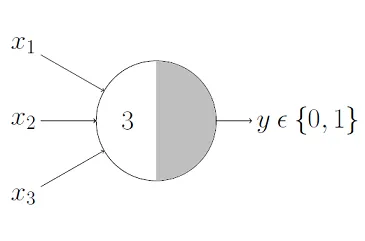
- the neuron fires only if all inputs are 1.
- or function
- the neuron fires if at least one input is 1.
- parameters:
- weights (𝑤1, 𝑤2,…): 1, 1,… (all equal to 1).
- threshold (𝜃): 1.
- weights (𝑤1, 𝑤2,…): 1, 1,… (all equal to 1).
- why? a single input firing (sum ≥ 1) is enough to cross the threshold.
- e.g. for 3 inputs, the neuron fires if 𝑥1 + 𝑥2 + 𝑥3 ≥ 1.
if either 𝑥1 = 1 or 𝑥2 = 1 or 𝑥3 = 1 (or all), the output is 1.
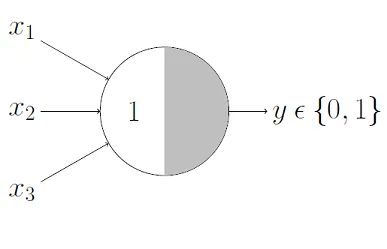
- the neuron fires if at least one input is 1.
- not function
- the neuron flips the input: outputs 1 if the input is 0, and 0 if the input is 1.
- parameters:
- weight (𝑤): -1.
- threshold (𝜃): 0.
- weight (𝑤): -1.
- why? if the input 𝑥 = 0, the sum (𝑤𝑥) = 0, which meets or exceeds the threshold, so the output is 1. if 𝑥 = 1, the sum (𝑤𝑥) = -1, which is below the threshold, so the output is 0.
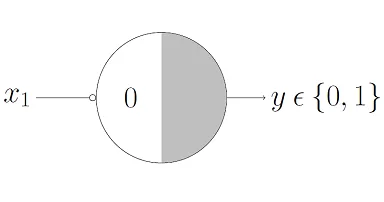
- the neuron flips the input: outputs 1 if the input is 0, and 0 if the input is 1.
- nor function
- the neuron outputs 1 only if all inputs are 0.
- parameters:
- weights (𝑤1, 𝑤2,…): -1, -1,… (all equal to -1).
- threshold (𝜃): 0.
- weights (𝑤1, 𝑤2,…): -1, -1,… (all equal to -1).
- why? if all inputs 𝑥1, 𝑥2,… are 0, the sum (𝑤1𝑥1 + 𝑤2𝑥2 + …) = 0, which meets or exceeds the threshold, so the output is 1.
if any input is 1, the sum becomes less than 0, so the output is 0.
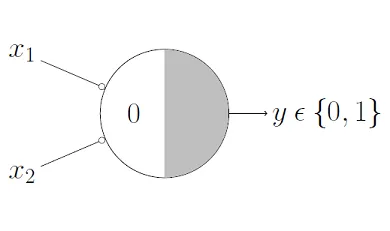
- the neuron outputs 1 only if all inputs are 0.
the perceptron
the perceptron, introduced by frank rosenblatt in 1958, is a foundational algorithm in machine learning used for binary classification. it improves upon the mcculloch-pitts neuron by introducing numerical weights for inputs and a mechanism to learn these weights from data. here’s a concise yet detailed explanation:
key concepts:
- inputs and weights:
- inputs (x1, x2, …, xn) can be any real-valued numbers (not just binary).
- each input is assigned a weight (w1, w2, …, wn), representing its importance.
- a bias term (w0) is added to shift the decision boundary, acting as a threshold or prior preference.
- activation function:
- the perceptron computes a weighted sum: z = Σ(from i=1 to n) wi xi + w0. (Note: Σ represents summation)
- it uses a step function to output:
y = 1 if z >= θ y = 0 otherwise - here, θ is the threshold (often set to 0).
- learning:
- the weights and bias are learned from training data.
- the perceptron adjusts weights iteratively to minimize classification errors.
example: movie preference
suppose you want to predict whether you’ll like a movie based on three binary inputs:
- isdirectornolan: 1 if directed by nolan, else 0.
- isactormattdamon: 1 if starring matt damon, else 0.
- isgenrethriller: 1 if the genre is thriller, else 0.
based on past data, you might assign:
- w1 = 3.0 (high weight for nolan),
- w2 = 1.0 (moderate weight for matt damon),
- w3 = 1.0 (moderate weight for thriller),
- w0 = -2.0 (bias, reflecting a moderate threshold).
for a movie with:
- isdirectornolan = 1,
- isactormattdamon = 0,
- isgenrethriller = 0,
the weighted sum is: z = (3.0 * 1) + (1.0 * 0) + (1.0 * 0) + (-2.0) = 1.0
if θ = 0, the perceptron outputs 1, meaning you would like the movie. the high weight for nolan allows the perceptron to cross the threshold even if other inputs are unfavorable.
limitations:
- linear separability: the perceptron can only classify data that is linearly separable.
- single-layer: it cannot model complex, non-linear relationships, which led to the development of multi-layer perceptrons (mlps) and deep learning.
difference from mcculloch-pitts neuron
-
the mcculloch-pitts neuron is a basic model that operates with fixed weights and strictly binary inputs and outputs. it follows predefined logical rules without any learning capability.
-
the perceptron can learn from data by adjusting its weights iteratively using the perceptron learning rule. this allows it to adapt to different patterns rather than being hardcoded for specific logic functions.
